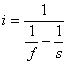Investigations Regarding Depth of Field (DOF)

Some Investigations

Regarding Depth of Field (DOF)

Working Draft / Thinking Notes

First Version December 19, 2005

Revised December {20,23,28}, 2005

Summary (“Tell ‘Em What You’re Gonna Tell ‘Em”)

The analysis described here confirms that smaller sensors give more DOF (at same f-number), shows that a long lens really does give a fuzzier background even when its DOF is effectively identical to a shorter lens, and shows that DOF’s for long and short lenses in fact are not exactly the same (although that’s a great approximation at short distances).

A simple rule of thumb is proposed that captures most (not all) of these effects:

DOF depends only on the angle subtended by the lens, as seen from the subject. Narrowing the angle gives proportionally larger DOF.

This is fascinating stuff. Despite being complicated and sometimes counterintuitive, these results are all derived from one basic optical law (the lens formula) and some simple geometry – with the aid of a spreadsheet. I love spreadsheets.

Background

At http://www.janrik.net/DOFpostings/PM1/Depth_of_Field_Versus_Sensor_Size.html , several pictures are posted that illustrate a smaller sensor camera giving more depth of field (DOF) than a larger sensor camera at same aperture, and equal DOF at a wider aperture.

These experimental results conflict with some (not all) statements at http://www.photomacrography1.net/forum/viewtopic.php?t=4026 , which firmly assert that DOF in a standard-size print is independent of sensor size.

Does Optical Law Allow & Explain Greater DOF from a Smaller Sensor?

The short answer is “yes, absolutely”.

To see why, let’s develop our own model from first principles, rather than following the traditional approach of just applying somebody else’s formulas. This reduces the risk that we will misapply a formula, or apply one that contains hidden assumptions or is only an approximation that does not apply under conditions we care about.

The model will not be complicated. All we need is some simple geometry, algebra, and one basic lens formula:

or equivalently,

where

f is the lens focal length

s is the distance to a point on the subject

i is the distance to the focused image of s

Our general strategy is to use this formula plus simple geometry to compute the blur circles for out-of-focus points as they would appear in a standard size print, given

· sensor size

· lens focal length

· f-number

· distance to subject

The formulas for this computation turn out to be quite simple.

We will create a spreadsheet from these formulas. Then we will play with the numbers to analyze the cases of interest, for example by determining the maximum near and far distances that produce tolerable blur circles, thus giving us the total DOF.

Using numbers in a spreadsheet with simple equations avoids the tedium and possible errors of doing algebra on complicated equations. In addition it gives us for free the ability to examine intermediate results, which often helps in trying to develop understanding. It also lets us explore extreme cases that may not be covered accurately by the standard formulas.

To derive our formulas, consider this diagram.

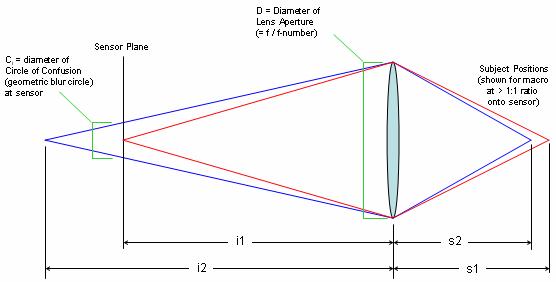
By the basic lens formula, we have that

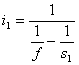and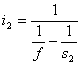

Let the sensor width be called w_s. Then the field width w_f is just

w_f = w_s * (s₁/i₁)

From the definition of f-number, we have that the aperture diameter D is

D = f / f-number

Then from simple geometry, we get that C_i, the diameter of the circle of confusion (blur circle) in the image plane is

C_i = abs(D * (i₂-i₁)/i₂)

(The absolute value is required to handle cases where i₂ < i₁ .)

Let the width of the standard print be called w_p. Then the magnification required for printing is w_p/w_w, so that C_p, the diameter of the blur circle in the print is just

C_p = (w_p/w_s) * C_i

That’s it – the whole model in 6 really simple equations. As a spreadsheet, it looks like this:

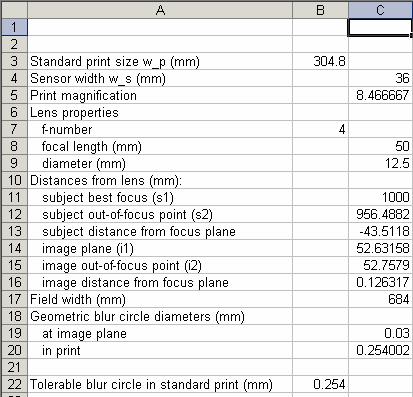
These formulas hide behind the scenes:

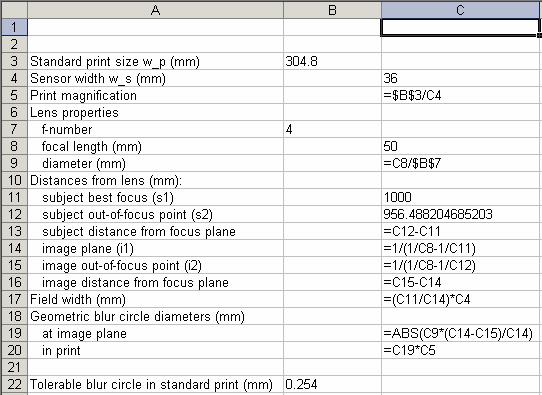
To check our work, let’s first see if we can reproduce some results from somebody else’s DOF calculator, say http://www.dofmaster.com/dofjs.html . This site specifies circle of confusion at the sensor, not in the print, but we can easily convert that. For 35mm film (24x36mm image), dofmaster says that the circle of confusion is 0.03mm. That scales to be 0.03*(304.8/36) = 0.254 mm = 1/100 inch for a 12-inch (304.8mm) print. That’s a standard number, and we’ll use it too: 0.254 blur circle in a 304.8mm print.

Pick a test case, say 35mm film, 50mm lens at f/4, 100 cm to subject. Then dofmaster says that the distances to near and far planes are 95.6 cm and 104.8 cm. Converting to mm and plugging those distances into our spreadsheet gives blur circles of 0.2570 and 0.2545 mm – pretty close to our target of 0.254mm!

We can play with the numbers in the spreadsheet to find more precise distances. Using the Excel Solver to jiggle the numbers automatically gives close focus of 956.49mm and far focus of 1047.9mm. So in fact our numbers agree with dofmaster to within rounding error. That’s encouraging. Total DOF is 91.4mm.

Let’s test with some different numbers. We’ll keep the same sensor size, change the distance to match the lens length, and see what happens. Stick with 35mm film, f/4.0, and we get these results: 50mm@100 cm, DOF 91.4mm; 100mm@200cm, DOF 91.3mm; 200mm@400cm, 91.2mm; 500mm@2000cm, DOF 91.2mm. All these agree both with dofmaster and with the standard “law” that DOF does not depend on lens length. (More about this as we near the end!)

Now let’s test in a different direction, keeping the distance the same while varying the sensor size and lens length to match.

With a bigger sensor: 6x9 film with a 125mm f/4 lens at 100cm. Dofmaster says 98.5 and 101.6 cm, total DOF 3.14 cm (31.4mm). Our spreadsheet says 983.52 and 1017.17 mm, total DOF = 33.6 mm. Still good agreement (though not quite exact, for unknown reasons).

With a smaller sensor: Canon Digital Rebel / 300D, sensor width 22.7mm, lens length 32mm, f/4, still at 100 cm to subject. Dofmaster says 14.4cm (144mm) depth of field, our spreadsheet says 143.8mm.

So our spreadsheet is still tracking right on with dofmaster, at least for these test cases.

And we’re getting clear evidence that DOF is larger with smaller sensor sizes (at same aperture).

Examining the spreadsheet numbers in closer detail provides an explanation for why DOF is larger with smaller sensors. Let’s fix the location of an out-of-focus point and look at what happens to the sensor and print blur circles as we change the sensor size.

Using the conditions just listed, we get this:

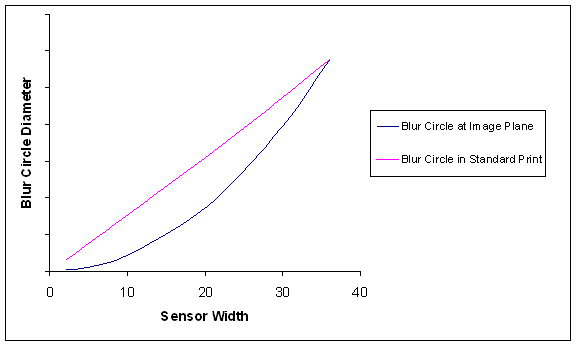
It’s apparent that under these constraints (keep f-number and distance the same, vary lens length to match sensor size), the blur circle at the image plane shrinks faster than the sensor size does. After magnifying to get a standard print, the blur circle in the print varies in direct proportion to the sensor size. Smaller sensor, much smaller blur circle, larger DOF, no problem. (All this assumes that our f-numbers are wide enough to avoid significant diffraction. But that’s a topic for another day.)

Another Inquiry – Do Long Lenses Make Backgrounds Fuzzier?

We can use this same spreadsheet technique to explore other issues surrounding DOF.

For example, it is part of standard photographic lore that long lenses do a better job of separating a subject from its background. But it’s also true that long lenses have the same DOF as short lenses, if you adjust the distance to keep the same size field. We showed that ourselves, a couple of pages earlier, right?

So what’s going on? Why do photographers think that long lenses give fuzzier backgrounds?

One possible explanation is that it’s purely a psychological effect, as suggested by the discussion of distant mesquite trees at http://www.oncloserinspection.com/Photomacrography/Photo_Myths/DOF1/DOF1.htm .

But perhaps there’s something more objective going on. Let’s look.

Rather that just considering the very small blur circles associated with DOF, let’s look at what a viewer would consider relevant: the large blur circles associated with distant background.

To have a specific example, let’s consider a fixed point 10 meters behind our subject, as we change lenses from 25 to 400 mm and move back to keep the same field of view for our in-focus subject. We already know that at f/4, the DOF is only 91.4mm, so this point 10 meters back is severely OOF. But what does “severely” mean? It’s not hard to find out – just plug the numbers into the spreadsheet and compute the blur circles. Here’s the result:

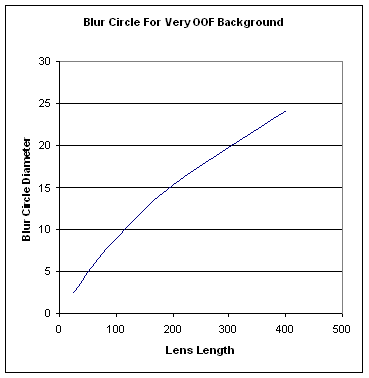
Aha! This graph gives us new insight. Yes, it’s true that for points close to the focus plane, the blur circle diameter does not vary with lens length. (Actually, it varies a tiny bit, but nothing you’d ever notice.) On the other hand, for distant background, longer lenses do in fact produce bigger blur circles, and bigger blur circles is equivalent to more OOF.

It is an interesting coincidence – an effect of the equations – that changes in blur circle size parallel the changes in scale quite closely, to within a few percent in this example. (Data not shown.) So our model confirms the observation at http://www.oncloserinspection.com/Photomacrography/Photo_Myths/DOF1/DOF1.htm that the OOF distant mesquite trees look the same with both lenses if you magnify them to the same scale. However, the difference in blur circle size provides a direct physical explanation for why the long lens’ background looks fuzzier. No psychological effects are needed.

It’s interesting to note that this effect (fuzzier backgrounds with a long lens) does not mean that you also get fuzzier foregrounds with long lenses. In fact, it works the other way around – OOF points in the foreground actually get sharper with longer lenses, though the effect is not so pronounced. For example, here’s the graph for a point that is 0.25 meters in front of our subject:

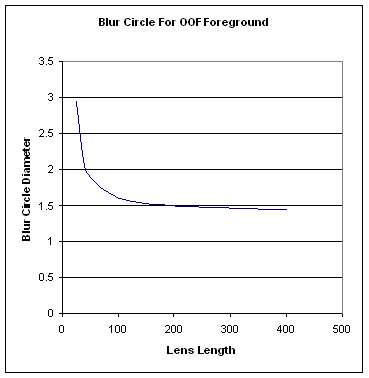
Do Long and Short Lenses Actually Have Identical DOF?

It’s often claimed that long and short lenses have identical DOF at same f-number, if you adjust the lens-to-subject distance to keep the subject size constant in the image. In fact, the author writing at http://en.wikipedia.org/wiki/Depth_of_field feels compelled to say “exactly the same”, complete with italics.

However, the claim that long and short lenses have identical DOF at the same subject size is in fact only approximate, although it is very close to exact at short distances. At longer distances the DOF’s of long and short lenses become progressively more different, with the long lens exhibiting less DOF in back of the subject plane, but more in front of it. For example:

40mm f/4 lens at 10 meters, front DOF = 5.7m, back DOF = 39.9m
400mm f/4 lens at 100 meters, front DOF = 6.9m, back DOF = 8.1m

So, revisiting the case of background 10m behind our subject, we may be more comfortable explaining that the background is simply beyond the range where the DOF's of long and short lenses are the same.

Proposal: A Simple Rule of Thumb

We have considered above the following two cases:

Case 1: Same f-number, same sensor size, change lens length and adjust distance to get same field of view. In this case DOF does not change.

Case 2: Same f-number, same distance, change sensor size and adjust lens length to get same field of view. In this case the smaller sensor and correspondingly shorter lens gives larger DOF.

This seems complicated and hard to keep straight. What we understand today, we are likely to scramble tomorrow.

Is there a simple rule of thumb that covers both cases? Fortunately, there is:

DOF depends only on the angle subtended by the lens, as seen from the subject. Narrowing the angle gives proportionally larger DOF.

Let’s see how to apply this rule.

In case 1, as we back up, using a longer lens at constant f-number, the diameter of the lens scales in proportion to the distance. The angle remains the same, and so does the DOF. The rule works.

In case 2, as we shrink the sensor and shorten the lens, the diameter of the lens shrinks while the distance remains constant. The angle gets narrower, and the DOF gets larger. The rule works again.

Again, this rule is only approximate. It doesn’t pick up the difference between long and short lenses at long distances. But still, it’s arguably better to have one simple rule than two complex rules.

Closing Comments (“Tell ‘Em What You Told ‘Em”)

A simple rule of thumb is proposed that captures most (not all) of these effects:

DOF depends only on the angle subtended by the lens, as seen from the subject. Narrowing the angle gives proportionally larger DOF.

Acknowledgement

Thanks are due to Charles Krebs for pointing out that long and short lenses have same DOF only at relatively short distances.

Related Reading

http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/lenseq.html#c2 and related pages have good diagrams and lens equations.

http://bobatkins.com/photography/technical/digitaldof.html and other pages at the same site have good discussions of DOF under various conditions.

http://bobatkins.com/photography/technical/depth_of_field_calc.html describes a very sophisticated depth-of-field calculator that apparently includes the effects of diffraction. (But only at infinity focus, not macro -- sorry!)

http://www.bobwheeler.com/photo/ViewCam.pdf is a very detailed analysis of DOF in numerous circumstances, including with lens tilts in a view camera. The treatment is primarily geometric and algebraic, with a few tables for illustration. The author cautions that “The reader should be warned that these notes do not comprise an exposition or tutorial but are simply a set of notes that were made while thinking through the problems. They are somewhat dense, and not recommended reading unless one really has to know.” [http://www.bobwheeler.com/photo/Documents/documents.html].

--Rik