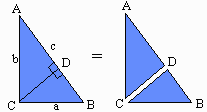 Consider any right triangle ABC.
Choose point D on the hypotenuse AB, such that line CD
is perpendicular to AB. Then the large right triangle
ABC is split into two smaller right triangles ADC and
BDC.
Consider any right triangle ABC.
Choose point D on the hypotenuse AB, such that line CD
is perpendicular to AB. Then the large right triangle
ABC is split into two smaller right triangles ADC and
BDC.
There are many ways to prove the Pythagorean Theorem. A particularly simple one is to use the scaling relationship for areas of similar figures.
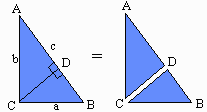 Consider any right triangle ABC.
Choose point D on the hypotenuse AB, such that line CD
is perpendicular to AB. Then the large right triangle
ABC is split into two smaller right triangles ADC and
BDC.
Consider any right triangle ABC.
Choose point D on the hypotenuse AB, such that line CD
is perpendicular to AB. Then the large right triangle
ABC is split into two smaller right triangles ADC and
BDC.
All three triangles have equal angles and are
therefore
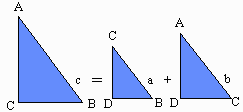 similar, so their
areas are related by the scaling formula:
similar, so their
areas are related by the scaling formula:
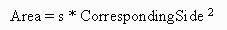
for some number "s" that is the same for
all three triangles.
(Scroll down to see the rest of the proof.)