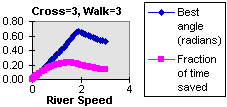
And in any case -- the time
that you save, and the best angle, depend
on the river speed in a complicated way. If you make graphs of
the best angle and the fraction of time saved, they look like this.
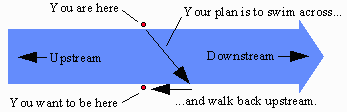Here's the situation.
You are standing on one bank of a river. You want to get
to the point exactly opposite, on the other bank.
You plan to do this in two stages. Stage one is to cross the river,
say by swimming or rowing a boat. As you cross, you'll get
swept downstream by the current. When you get to the other
side, you plan to walk back
upstream to your destination. Walking upstream is stage two.
It occurs to you that you might save some time by pointing upstream while crossing the river. It will take a little longer to cross the river that way, but you won't get swept downstream so far. That means less time walking back upstream, and you hope to come out ahead overall.
Does this actually work? If it does, then how much time can you save, and under what conditions? (Continue to see some answers.)
And in any case -- the time
that you save, and the best angle, depend
on the river speed in a complicated way. If you make graphs of
the best angle and the fraction of time saved, they look like this.
The general strategy is like this:
Before going on, you may want to go play with a simple spreadsheet that calculates the trip time or the spreadsheet that we used to make the graph on the previous page. (Go on, to start looking at the math.)
When we've got the first 7 formulas in hand, we'll use them to look at the problem in several ways.
Now, on to the math!
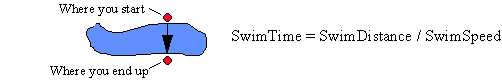
But it may not be so easy to see how this formula applies to the problem of swimming (or canoeing) at some angle across a river. There are two difficulties:
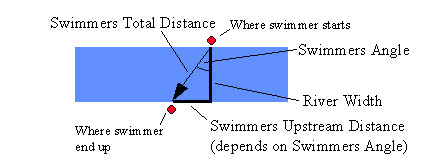
Let's look at that picture again.
The figure is a right triangle, so both the
Pythagorean Theorem and
basic trigonometry functions are
easy to apply.
Since you may not know any trigonometry yet, let's proceed by specifying Swimmers Upstream Distance. Then we can compute Swimmers Total Distance using the Pythagorean Theorem. In the notation used by Excel (and many other computer programs), this is
But that's OK -- the pieces we need are simple, and you'll be needing them often anyway. What we have here is a typical application -- find the angles of a right triangle when you know the lengths of its sides.
You can go review the
basic trigonometry functions
to see how they work in general. The one we need here is
arcsine (spelled "asin"
in Excel and most other computer languages).
This lets us find an angle
when we know the lengths of the hypotenuse and the side
opposite the angle.
The final catch is that we need to be careful about the units that
we to measure angles. In math. including most calculators and
spreadsheets, angles are usually measured
radians. But if you prefer degrees,
just multiply radians by 180/pi.
(Next: what is the effect of the water moving?)
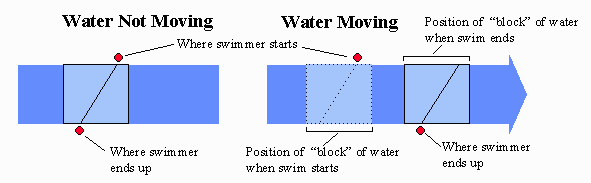So, your time to cross the river is the same as if the river
were not flowing, even though you may drift quite a ways downstream.
(Continue)
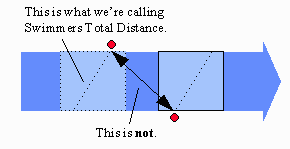Just remember, though --
this distance and speed refer to the
water that the swimmer moves through.
They do not include the extra distance and speed due to
the swimmer being swept along with
the block of water.
(Next: how far do you end up downstream?)
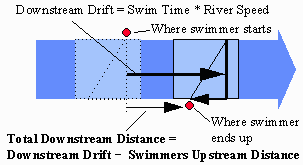The strategy is to figure out far the block of water drifts
downstream, by using the River Speed and the Swim Time (which
we calculated earlier).
Then we subtract the Swimmers Upstream Distance
(remember, this is measured relative to the block of water),
from the block of water's Downstream Drift.
This difference is your Total Downstream Distance, which is how far you have to walk back upstream.
Now we're ready to look at
walk time and total travel time.
For the first part, all we have to do is time = distance / speed:
Wasn't that a refreshing break?
Next: All the Formulas at Once
When all these formulas get crammed together like this, they look complicated.
But they aren't, really.
Remember how we got here?
Each formula was just one application of some simple idea.
Let's look at those ideas again.
(Continue.)
Simple ideas, applied one at a time. The end result looks complicated, but it's just a bunch of simple ideas applied one after another.
Let's go plug in some numbers.
(Continue.)
When you derive formulas, it's always a good idea to plug in numbers, run through the formulas "by hand", and see if the results make sense. If they do, then there's a good chance that you got the formulas right. And if they don't, well, back to the drawing board! Maybe you made a mistake in deriving the formula, or maybe you evaluated wrong, or maybe your idea of "making sense" is wrong. They all happen, and frequently -- at least in the author's experience!
These "numerical checks" are very important. It's easy to make mistakes in deriving formulas, and even easier to overlook the mistakes when you check the math later. But if you plug in numbers, and the numbers don't make sense, errors in the formulas are likely to become obvious.
We think our formulas are correct, but you really ought to haul out a calculator and run through them to be sure. For example, if you plug in River Speed = 3, River Width = 0.1, Swim Speed = 0.5, Walk Speed = 3, and Swimmers Upstream Distance = 0.02, then you ought to end up with Total Time = 0.4013 . (We'll let you figure out what the other answers are!)
Now, let's go on to put these formulas in a
simple swim-and-walk spreadsheet.
You can save a lot of trouble by putting the formulas into a spreadsheet program, like Microsoft Excel. Spreadsheet programs remember the formulas that you type in. Then, when you put in numbers, the spreadsheet automatically recalculates the formulas. You can also set up the spreadsheet to make graphs of your numbers. When you put in new numbers, the graphs will get updated automatically, too.
There are lots of ways that you could put the spreadsheet together. We put together a simple one to illustrate how formulas work. Please go explore our spreadsheet to see how it works and how it's put together.